Posit AI Blog: Community spotlight: Fun with torchopt

From the beginning, it has been exciting to watch the growing number of packages being developed in the torch ecosystem. The variety of things people do is amazing torch: expand its functionality; integrate and use domain-specifically its low-level automatic differentiation infrastructure; port architectures of neural networks … and last but not least, to answer scientific questions.

This blog post will introduce one of these packages in a brief and rather subjective form: torchopt. Before we start, there’s one thing we should probably say a lot more often: If you’d like to publish a post on this blog, about a package you’re developing, or about how you use deep learning frameworks in R, let us know – you’re more than welcome!

torchopt

torchopt is a package developed by Gilberto Camara and colleagues at the National Institute for Space Research in Brazil.

From the looks of it, the reason the pack exists is pretty self-explanatory. torch itself does not – nor should it – implement all newly published optimization algorithms potentially useful for your purposes. So the algorithms compiled here are probably exactly the ones the authors were most eager to experiment with in their own work. At the time of writing, they understood various members of the people among others ADA* and *ADAM*families. And we can safely assume that the list will grow over time.

I’ll introduce the package by highlighting something that is technically “only” a utility feature, but can be extremely useful to users: the ability for any optimizer and any test function to plot the steps taken in the optimization.

While it’s true that I don’t intend to compare (let alone analyze) different strategies, there is one that I think stands out in the list: ADAHESSIAN (Yao et al. 2020), a second-order algorithm designed to scale to large neural networks. I’m especially curious how it compares to L-BFGS, the second-order “classic” available from base torch last year we had a special blog post.

The way it works

The utility in question is named test_optim(). The only required argument refers to the optimizer to try (optim). However, you’ll probably want to tweak three more as well:

• test_fn: To use a test function other than the default (beale). You can choose from many offered in torchopt, or you can submit your own. In the latter case, you must also provide information about the search domain and starting points. (We’ll see that in a moment.)
• steps: Setting the number of optimization steps.
• opt_hparams: Adjust optimizer hyperparameters; especially the speed of learning.

I will use here flower() a feature that already figured prominently in the aforementioned post on L-BFGS. It approaches its minimum as it approaches it (0,0) (but not defined in the origin itself).

Here it is:

flower <- function(x, y) {
  a <- 1
  b <- 1
  c <- 4
  a * torch_sqrt(torch_square(x) + torch_square(y)) + b * torch_sin(c * torch_atan2(y, x))
}

Scroll down a bit to see what it looks like. The plot can be modified in countless ways, but I’ll stick with the default layout with shorter wavelength colors mapped to lower function values.

Let’s begin our explorations.

Why do they always say that learning speed matters?

True, it’s a rhetorical question. But still, sometimes visualizations provide the most memorable evidence.

Here we use the popular first-order optimizer, AdamW (Loshchilov and Hutter 2017). We call this the default learning rate, 0.01and let the search run two hundred paces. As in the previous post, we will start from a distance – from a point (20,20)well outside the rectangular area of ​​interest.

library(torchopt)
library(torch)

test_optim(
    # call with default learning rate (0.01)
    optim = optim_adamw,
    # pass in self-defined test function, plus a closure indicating starting points and search domain
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    steps = 200
)

Oops, what happened? Is there a bug in the rendering code? – Not at all; it’s just that we haven’t entered the area of ​​interest after the maximum number of steps allowed.

Next, we increase the learning rate by a factor of ten.

test_optim(
    optim = optim_adamw,
    # scale default rate by a factor of 10
    opt_hparams = list(lr = 0.1),
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    steps = 200
)

What has changed! With ten times the learning speed, the result is optimal. Does this mean the default is bad? Of course not; The algorithm was tuned to work well with neural networks, not some function that was deliberately designed to pose a particular challenge.

Of course, we also have to see what happens for even higher learning rates.

test_optim(
    optim = optim_adamw,
    # scale default rate by a factor of 70
    opt_hparams = list(lr = 0.7),
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    steps = 200
)

We’re seeing the behavior we’ve always been warned against: The optimization jumps wildly before seemingly going forever. (Apparently, because in this case it won’t. Instead, the search will jump far and back, continuously.)

Now someone might be interested. What actually happens if we choose a “good” learning rate but don’t stop optimizing after two hundred steps? Here we try three hundred instead:

test_optim(
    optim = optim_adamw,
    # scale default rate by a factor of 10
    opt_hparams = list(lr = 0.1),
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    # this time, continue search until we reach step 300
    steps = 300
)

Interestingly, the same kind of back-and-forth occurs here as with the higher learning rate—it’s just delayed in time.

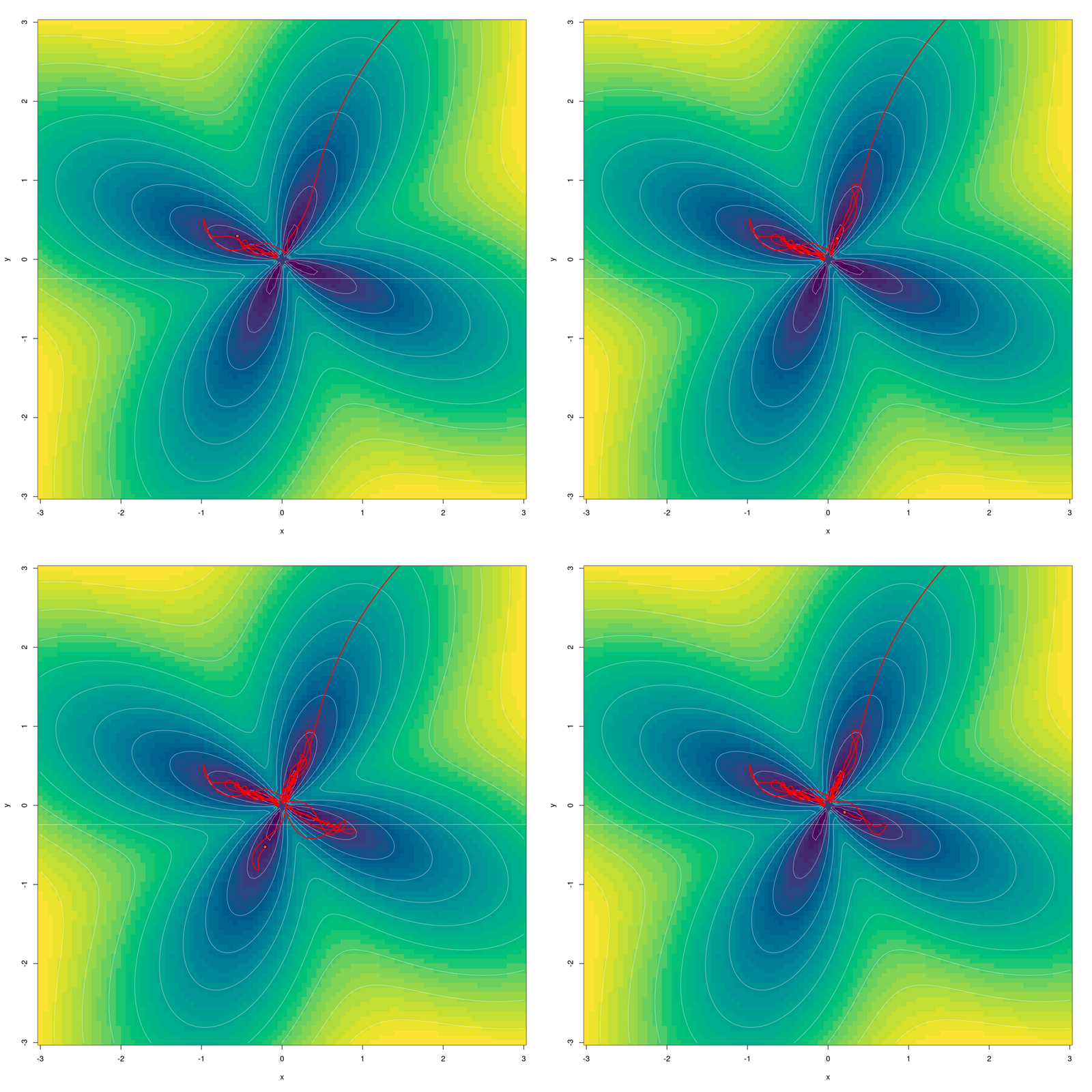
Another playful question that comes to mind is: Can we watch the optimization process “explore” the four petals? Through some quick experimentation I came up with this:

Who says you need chaos to create a beautiful plot?

A second-order optimizer for neural networks: ADAHESSIAN

On to one algorithm I’d like to look at specifically. After a little experimentation with the learning rate, I was able to arrive at an excellent result after only thirty-five steps.

test_optim(
    optim = optim_adahessian,
    opt_hparams = list(lr = 0.3),
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    steps = 35
)

Given our recent experience with AdamW – that is, it “just doesn’t settle” very close to the minimum – we may want to do an equivalent test with ADAHESSIAN as well. What happens if we continue the optimization a bit longer – say two hundred steps?

test_optim(
    optim = optim_adahessian,
    opt_hparams = list(lr = 0.3),
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    steps = 200
)

Like AdamW, ADAHESSIAN continues to “explore” the petals but doesn’t stray as far from the low.

Is it surprising? I wouldn’t say yes. The argument is the same as AdamW’s above: His algorithm was tuned to work well on large neural networks, not to solve the classical, hand-crafted minimization task.

Now that we’ve heard this argument twice, it’s time to verify the explicit assumption: that the classical second-order algorithm does it better. In other words, it’s time to revisit L-BFGS.

The best of the classics: Revisiting the L-BFGS

Use test_optim() with L-BFGS we have to digress a bit. If you’ve read the post on L-BFGS, you may recall that with this optimizer it is necessary to wrap both the test function call and the gradient evaluation in a closure. (The reason is that both must be callable multiple times per iteration.)

Now that we see how L-BFGS is a very special case that probably few people use test_optim() in the future it would not seem appropriate for this function to handle different cases. For this on-off test, I simply copied and modified the code as needed. Result, test_optim_lbfgs()can be found in the attachment.

When deciding what number of steps to try, we consider that L-BFGS has a different concept of iterations than other optimizers; that is, it can refine its search several times per step. In fact, I happen to know from a previous post that three iterations are enough:

test_optim_lbfgs(
    optim = optim_lbfgs,
    opt_hparams = list(line_search_fn = "strong_wolfe"),
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    steps = 3
)

At this point, of course, I have to stick to my rule of testing what happens with “too many steps”. (Although this time I have good reason to believe that nothing will happen.)

test_optim_lbfgs(
    optim = optim_lbfgs,
    opt_hparams = list(line_search_fn = "strong_wolfe"),
    test_fn = list(flower, function() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
    steps = 10
)

Hypothesis confirmed.

And here my playful and subjective introduction ends torchopt. I sure hope you enjoyed it; but in any case, I think you should have gotten the impression that here is a useful, extensible, and probably expanding package to keep an eye on in the future. As always, thanks for reading!

Appendix

test_optim_lbfgs <- function(optim, ...,
                       opt_hparams = NULL,
                       test_fn = "beale",
                       steps = 200,
                       pt_start_color = "#5050FF7F",
                       pt_end_color = "#FF5050FF",
                       ln_color = "#FF0000FF",
                       ln_weight = 2,
                       bg_xy_breaks = 100,
                       bg_z_breaks = 32,
                       bg_palette = "viridis",
                       ct_levels = 10,
                       ct_labels = FALSE,
                       ct_color = "#FFFFFF7F",
                       plot_each_step = FALSE) {


    if (is.character(test_fn)) {
        # get starting points
        domain_fn <- get(paste0("domain_",test_fn),
                         envir = asNamespace("torchopt"),
                         inherits = FALSE)
        # get gradient function
        test_fn <- get(test_fn,
                       envir = asNamespace("torchopt"),
                       inherits = FALSE)
    } else if (is.list(test_fn)) {
        domain_fn <- test_fn((2))
        test_fn <- test_fn((1))
    }

    # starting point
    dom <- domain_fn()
    x0 <- dom(("x0"))
    y0 <- dom(("y0"))
    # create tensor
    x <- torch::torch_tensor(x0, requires_grad = TRUE)
    y <- torch::torch_tensor(y0, requires_grad = TRUE)

    # instantiate optimizer
    optim <- do.call(optim, c(list(params = list(x, y)), opt_hparams))

    # with L-BFGS, it is necessary to wrap both function call and gradient evaluation in a closure,
    # for them to be callable several times per iteration.
    calc_loss <- function() {
      optim$zero_grad()
      z <- test_fn(x, y)
      z$backward()
      z
    }

    # run optimizer
    x_steps <- numeric(steps)
    y_steps <- numeric(steps)
    for (i in seq_len(steps)) {
        x_steps(i) <- as.numeric(x)
        y_steps(i) <- as.numeric(y)
        optim$step(calc_loss)
    }

    # prepare plot
    # get xy limits

    xmax <- dom(("xmax"))
    xmin <- dom(("xmin"))
    ymax <- dom(("ymax"))
    ymin <- dom(("ymin"))

    # prepare data for gradient plot
    x <- seq(xmin, xmax, length.out = bg_xy_breaks)
    y <- seq(xmin, xmax, length.out = bg_xy_breaks)
    z <- outer(X = x, Y = y, FUN = function(x, y) as.numeric(test_fn(x, y)))

    plot_from_step <- steps
    if (plot_each_step) {
        plot_from_step <- 1
    }

    for (step in seq(plot_from_step, steps, 1)) {

        # plot background
        image(
            x = x,
            y = y,
            z = z,
            col = hcl.colors(
                n = bg_z_breaks,
                palette = bg_palette
            ),
            ...
        )

        # plot contour
        if (ct_levels > 0) {
            contour(
                x = x,
                y = y,
                z = z,
                nlevels = ct_levels,
                drawlabels = ct_labels,
                col = ct_color,
                add = TRUE
            )
        }

        # plot starting point
        points(
            x_steps(1),
            y_steps(1),
            pch = 21,
            bg = pt_start_color
        )

        # plot path line
        lines(
            x_steps(seq_len(step)),
            y_steps(seq_len(step)),
            lwd = ln_weight,
            col = ln_color
        )

        # plot end point
        points(
            x_steps(step),
            y_steps(step),
            pch = 21,
            bg = pt_end_color
        )
    }
}